Subsections
Although the DNASAND and the ZEBRA algorithm do not specify the overall type
of global relationship of two sequences (total correspondence, containment or
overlapping, see Huang (1994)), any type of relationship is recognised. As
result of this first scan, a hash storing technique is used to represent
sparse matrices containing information on potential overlaps of all the
fragments and their orientation (forward-forward or forward-complement) is
generated. Figure 23 shows a schematic drawing on how these
data structures are interpreted internally.
Figure 23:
The ``matrices'' generated after the first
fast scan of every read against every other in search for potential
overlaps. Unlike this small example with 6 reads might suggest, the
matrices in real world projects - with a large number of reads - are
normally sparsely occupied. Therefore, using hash storing techniques is
more appropriate as otherwise memory consumption would explode for
larger number of reads.
|
![\includegraphics[width=\textwidth]{figures/aaamatrix}](img110.png)
|
In the next fundamental step, these potential overlaps found during the
scanning phase must be examined more thoroughly. Several algorithms have bee
devised for alignments of multiple sequences: Allison (1993) devised a
divide-and-conquer technique for aligning three strings, Stoye (1998) used a
similar technique for 6 to 12 strings. But these multiple alignment
algorithms are still too slow (see Gotoh (1993) for a good explanation) to
be used in an assembly match inspection phase, even when parallelised multiple
alignment algorithms run on multiple processors like Kleinjung et al. (2002)
presented.
In the end, the strategy devised for the mira assembler works by
examining potential matches two at a time with a modified Smith-Waterman
algorithm for local alignment of overlaps. Similar
strategies were extensively studied by Barton (1993) and have found their
way into other current assemblers like, e.g., PGA (Paracel (2002b)).
Improving Smith-Waterman alignment by banding
Observe that two sequences
that align well will generate a path through a Smith-Waterman alignment matrix
that will almost run diagonally from the entry point to the exit point. Only
indels will cause a horizontal or vertical shift of the alignment graph.
Assuming that one knew the approximate whereabouts of either the entry or the
exit point and that the alignment has 'acceptable' quality, i.e. not too many
indels that are spread unilaterally in one of the sequences. It is then a
valid assumption that it should be feasible to reconstruct the alignment by
calculating only the narrow corridor (a band) through the matrix where the
alignment graph is expected to run through, as is shown in figure
24.
A bonus information not to be underestimated is the fact that both DNASAND and
ZEBRA not only provide the information whether two sequences are similar
enough to try a sequence alignment, but they also provide the approximate
offset for the sequence alignment. This information is valuable because it
locates the approximate entry points of such an alignment in the alignment
matrix and therefore allows to reduce the computational complexity - and
with it the time needed - for a SW alignment with two sequences drastically.
Figure 24:
Smith-Waterman banding. n1 and n2
are the length of the sequences. Instead of computing the whole matrix
(n1*n2 cells), only a small band within the approximated area of the
overlap must be computed: o is the approximated offset from sequence 1
to sequence 2 in the alignment, m the approximated length of the
overlap and k the band width to be calculated. s is the predicted
starting point for the recursive path drawing algorithm and e the
predicted exit area.
|
![\includegraphics[width=8cm]{figures/SWband}](img111.png) |
Let n1 and n2 be the length of the sequences, m the approximate length
of the overlap and k a safety margin of indels that might arise in the
alignment of the overlap. It is clear that
m 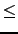 min
min(
n1,
n2)
is always true for every possible configuration of m, n1 and n2.
Furthermore one can assign k to be
k =
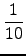
*
m where typically 30
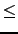 k
k 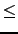
70
The higher k, the more tolerant the algorithm will be regarding slightly
false approximations of alignment path entry-points or the more
non-compensated indels can occur in one of the sequences. Using the values
mentioned above ensures a sufficiently wide and adaptable security margin for
the length of sequences that have to be aligned in a shotgun assembly while
keeping k linear within bounds.
While the normal Smith-Waterman alignment will need
O(n1*n2)
time to compute the alignment matrix, the banded version will need only
O(
k*
m)
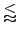 O
O(
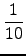 m2
m2)
to compute the band through the matrix where the alignment is supposed to be.
For n1, n2 being typically between 300 and 1200 and normally
m 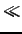 n1
n1*
n2
so O(k*m) can be seen to have mostly a less than linear complexity compared
to the square complexity of
O(n1*n2).
Note that although methods for linear-space alignment methods have been
devised23, these have not been implemented for the time being as typical
shotgun fragment lengths are small enough to allow quadratic space algorithms.
Figure 25:
Smith-Waterman band prediction. According to the offset
prediction from DNASAND and ZEBRA-BLOCKING (examples o1, o2 and
o3 in the figure), different bands can be computed, all differing in
length. These examples show particularly well how the O(n2)
Smith-Waterman calculation of a matrix can be effectively scaled down to
less than O(n).
|
![\includegraphics[width=\textwidth]{figures/SWbandpred}](img116.png) |
The changes needed to adapt the SW algorithm are minimal. A small logical
overhead is needed to segment the band and the matrix to facilitate
computation. Additionally - and assuming the alignment matrix is calculated
row by row - the left and right edge of each row must calculated with a
slightly adapted algorithm to take care that the recursive alignment algorithm
afterwards will not run out of the band.
Cells outside the calculated band are assigned to have a very high value, e.g.
the INTMAX value, which is defined to be the highest integer value
that can be represented within a given integer datatype. In practice, to avoid
the O(n2) complexity of filing the whole matrix, only the matrix cells
adjacent to the calculated band are initialised. This constitutes a 'fence'
that the recursive path alignment algorithm will not be able to transgress
later on and make sure that all alignments found later will stay within the
calculated band.
Figure 26:
Smith-Waterman (SW) band calculation predecessor rules. The figure
shows a section of a larger SW matrix. The grey cells represent the
border of the band within the matrix, arrows show the predecessor cells
needed to compute a cell. Most cells in a band will be of type (a),
i.e., cells with normal predecessor rules like in a normal SW matrix.
Cells on the border of the band (b) and (c) need special handling as
they only have two (different) predecessor cells instead of three.
|
![\includegraphics[width=8cm]{figures/SWbandcalc}](img117.png) |
The calculation of cells that are not on the edges (the 'a' cell in figure
26) is performed like in a normal SW algorithm:
while each cell on the left edge in a row (the 'b' cell in figure
26) must not consider the fence value to
its left and consequently is calculated using
Similarly, each cell on the right edge in a row (the 'c' cell in figure
26) must not consider the fence
value to its top, so that the calculation is done using
Parametrising Smith-Waterman alignment
Several scoring schemes
for SW alignments have been devised within the last two decades, ranging from
the simple original one (Smith et al. (1981)) to methods accounting for gap
lengths using affine gap calculation and even alignments of sequences against
trace signals. Most publications that appeared analyse and discuss the
complexity of dynamic programming and scoring functions. Even very formal but
systematic and generally applicable methods to build early prototypes for
these algorithms were presented (see also Giegerich (2000)).
Althaus et al. (2002) proposed a multiple sequence alignment (MSA) with arbitrary
gap costs which computes an optimal solution using polyhedral combinatorics,
but having only two sequences at a time to score.
Arslan et al. (2001) presented a method that used iterated Smith-Waterman
computations with fractional programming with a run time of
O(n2log(n)) -
which is already higher than the O(n2) of standard Smith-Waterman - to
normalise the score of sequence alignments. Their experimental results
suggested that the number of required iterations were small, but they could
not establish a satisfactory theoretical lower- / average- / upper-bound for
the growth in the number of iterations needed.
Good alignments base on an appropriately chosen scoring scheme given to an
optimisation model. A slightly improved original Smith-Waterman scoring
scheme has been opted for simplicity, speed and sufficient sensitivity and
specificity of a first alignment approximation. The Smith-Waterman alignment
algorithm uses the weight matrix W given in table 2 to
calculate an alignment
score.
[Used SW scoring weight matrix]Extend version of the matrix shown
in table
1. Here, comparisons of
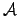 b
b
with endgaps (
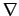
) or with ``N'' are score neutral.
| |
A |
C |
G |
T |
N |
* |
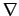 |
| A |
1 |
-1 |
-1 |
-1 |
0 |
-2 |
0 |
| C |
-1 |
1 |
-1 |
-1 |
0 |
-2 |
0 |
| G |
-1 |
-1 |
1 |
-1 |
0 |
-2 |
0 |
| T |
-1 |
-1 |
-1 |
1 |
0 |
-2 |
0 |
| N |
0 |
0 |
0 |
0 |
0 |
-2 |
0 |
| * |
-2 |
-2 |
-2 |
-2 |
-2 |
0 |
0 |
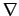 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
As can be seen by the values of W, this scoring scheme reflects ideally the
requirements that alignments of shotgun sequences with some degree of
errors contained: one can assume
a 'mismatch' of a base against a 'N' (symbol for aNy base) to have no penalty
as in many case the base caller rightfully set 'N' for a real, existing base
(and not an erroneous extra one) that could not be resolved further. But to
show that this still constitutes a minor reason for being careful, a 'N' gets
a neutral score instead of a match.
The scoring algorithm can be improved further by taking into account that -
regarding the fact that todays base callers have a low error rate - the
block-indel model (see Giegerich and Wheeler (1996)) does not
apply to the alignment of shotgun sequencing data: long stretches of
mismatches or gaps in the alignment are less probable than small, punctual
errors. In fact, more than two gap symbols following each other in an
alignment of shotgun sequences is a distinct signal that either the sequences
should probably not be assembled together or that something went wrong in the
laboratory or during signal processing (base calling). For this reason, a
configurable penalty function has been added that
scales down the score calculated through the scoring matrix W in
relationship to the number and length of gaps within an alignment. The
penalties used are shown in table 3. This is a
post-processing normalisation algorithm which is not dissimilar to the methods
proposed by Pearson (1995) and Shpaer et al. (1996).
[Default gap length penalty scores]Default penalty scores
inflicted to the score calculated with a weight
matrix. Each gap of a given length reduces the original score by
a specified penalty.
| gap length in bases |
penalty in % |
| 1 |
0 |
| 2 |
5 |
| 3 |
10 |
| 4 |
20 |
| 5 |
40 |
| 6 |
80 |
| 7+ |
100 |
In addition, a second score - the expected score - is calculated using the
score matrix represented in table
4.
Scoring weight matrix for the expected score
| |
A |
C |
G |
T |
N |
* |
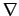 |
| A |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
| C |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
| G |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
| T |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
| N |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
| * |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
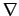 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
It can be deduced by the matrix values that this second score represents the
score expected if the alignment was perfect, i.e., without errors.
Consequently
score 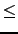 scoreexpected
scoreexpected
is always fulfilled. Note that it is not possible to take the length of the
overlap as expected score, because 'N' bases are treated as neutral in score
calculation. They therefore cannot get a better score in the calculation of
the expected score as this would mean there is an error although it is still
assumed that an 'N' is a correctly found base.
It is now trivial to make a ``rough guess'' of the alignment
quality of the overlap by calculating the score
ratio.
Rs =
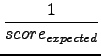
*
score with
Rs = 0 for
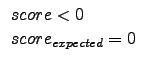
and therefore
0
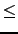 Rs
Rs 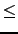
1
A problem left open up to now is the question on how to subsume the different
quality criteria i) length of the overlap and ii) score ratio into one
pregnant figure (the overlap weight) so that overlaps can be ranked easily and
comprehensibly.
The simplest method would be to multiply both values to get a weighted length
of the overlap. Let leno be the length of the overlap, so the desired
weight wo of this overlap could be computed by
wo = leno*Rs
But this approach attributes far too much weight to the length than it does to
the score ratio, which is - after all - the predominant measure for the
quality. For example, an overlap of length 650 bases with a score ration of
only 0.65 (65% similarity) would get a higher weight (422) than an undeniably
better overlap of length 400 bases and a score ratio of 0.9 (90% similarity,
weight: 360). This problem can be easily circumvented by squaring the score
ratio, giving it more importance in the calculation:
wo =
leno*
 Rs
Rs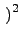
The first overlap would then get a weight of 274 and the second 324, which is
exactly the desired outcome.
Every candidate alignment overlap pair whose score ratio is within a
configurable threshold (normally upward of 70% to 80%) and where the length
of the overlap is not too small is accepted as 'true' overlap, candidate pairs
not matching these criteria - often due to spurious hits in the scanning
phase - are identified and rejected from further assembly (see figures
27 and 28).
Figure 27:
A modified Smith-Waterman algorithm for local alignment is used to
confirm or reject potential overlaps found in the fast scanning
phase. Accepted overlaps get a weight assigned depending on the length of
the overlap and alignment quality.
![\includegraphics[width=6.5cm]{figures/SWok}](img129.png)
|
Figure 28:
Although
having a good partial score, the overall score ratio of
this alignment is too low to be accepted. This read pair is eliminated
from the list of possible overlaps.
![\includegraphics[width=6.5cm]{figures/SWnok}](img130.png)
|
The overlap alignment - along with complementary data (like orientation of
the aligned reads, overlap region, score, score ratio etc.) - is called an
aligned dual sequences (ADS). Every ADS that passed the
Smith-Waterman test is kept in memory to facilitate and speed up the next
phases. Good alternatives are also stored to enable alternative alignments to
be found later on in the assembly.
All the ADS form one or several weighted graphs which
represent the totality of all the assembly
layout possibilities of a
given set of shotgun sequencing data (see figure 29). The
nodes of the graph are represented by the reads. An edge
between two nodes indicates that these two reads are at least partially
overlapping and can be aligned. Each graph sketches the alignment
possibilities of reads for at least one contig. Hence, the number of
non-connected graphs is equivalent to the minimum number of
contigs the assembler will be able to build.
Figure 29:
An overlap graph generated from the
aligned overlaps that passed the Smith-Waterman test. The thickness of
the edges represents the weight of an overlap. Although the (1,6) overlap
is marked for demonstration purposes in this figure, rejected overlaps
(due to spurious hits in the scanning phase, see figure
23) are not present in the graph.
|
![\includegraphics[width=\textwidth]{figures/pathgraph}](img131.png) |
The edges themselves are attributed with the score weights
computed for the overlaps and stored in the ADS.
Bastien Chevreux
2006-05-11
![\includegraphics[width=\textwidth]{figures/aaamatrix}](img110.png)
![\includegraphics[width=8cm]{figures/SWband}](img111.png)
![\includegraphics[width=\textwidth]{figures/SWbandpred}](img116.png)
![\includegraphics[width=8cm]{figures/SWbandcalc}](img117.png)



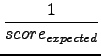 *score with Rs = 0 for
*score with Rs = 0 for 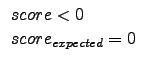
![\includegraphics[width=6.5cm]{figures/SWok}](img129.png)
![\includegraphics[width=6.5cm]{figures/SWnok}](img130.png)
![\includegraphics[width=\textwidth]{figures/pathgraph}](img131.png)