Building contigs

The overlaps found and verified in the previous phases must then be assembled into contigs. This is the most fundamental and intricate part of the process, especially in projects containing many repetitive elements. Several basic approaches to the multiple alignment problem have been devised to tackle this problem. Although algorithms for aligning multiple sequences at once have been used with increasing success lately for up to 10 to 15 sequences (Stoye (1998)), the amount of time needed to perform this alignment is still too unpredictable - ranging from a few seconds to several hours - to be used in sequence assembly.

Reinert et al. (2000) conducted experiments on iterative methods for faster sum-of-pairs with a divide-and-conquer alignment approach (using a $\ensuremath{\mathcal{A}}\,{}^*$ algorithm) and quasi-natural gap costs for multiple sequence alignments. Schlosshauer and Ohlsson (2002) devised an algorithm based on fuzzy recast of dynamic programming algorithms in terms of field annealing to score the reliability of sequence alignments. These methods also show varying runtimes ranging from a few seconds to hours for a relatively low number of sequences, far lower that the realistic number of sequences encountered in real world assembly projects.

Due to these problems, it was decided to use iterative pairwise sequence alignment and devise new methods for searching overlap candidates. A key concept is empowering contigs to accept or reject reads presented to them during the contig building. The algorithm consists mainly of two objects which interact with each other: a pathfinder module and a contig building module.

Pathfinder and contig interaction

Because an iterative approach is used to the multiple alignment problem - this means one always successively aligns an existing consensus against the next read - the results of the alignment sensitively depends on the order of pairwise alignments (Morgenstern et al. (1996)). As a direct consequence it is therefore preferable to build contigs using overlaps with reliable and high quality first and then continue with lower quality.

Hence, one has to make sure to start at the position in the contig where there are as many reads as possible with almost no errors. The pathfinder will thus - in the beginning - search for a node in the weighted graph having a maximum number of highly weighted edges to neighbours. The idea behind this behaviour is to take the read with the longest and qualitatively best overlaps with as many other reads as possible and use this one to ensure a good starting point: the 'anchor' for this contig.

A necessary constraint proved to be that the weight of the edges selected must not fall below a certain threshold as it is not infrequent to have a considerable number of relatively short reads with repetitive element contained in many projects. This introduces a sort of 'gravity well' in the assembly graph and misleads the algorithm to take a read with dangerous repetitive characteristics as anchor, which is generally not the intended behaviour.

The next step consists of determining the next read to add to the now existing contig by analysing nodes (reads) from the contig in the graph and determine which edge (overlap) with a node - not belonging to the contig - provides the most profitable overlap to augment the information contained within the contig.

There are theoretically two distinct approaches to perform this operation:

1. Backbone strategy: extend the existing contig in length with new, formerly not present data at the extremities of the contig
2. In-depth coverage strategy: improve the quality of the existing consensus by adding reads that increase coverage and thus increase base probabilities in the consensus

Both approaches have their specific advantages and disadvantages which will be discussed briefly.

Extending the contig length first implies the quality of the reads to be reliably high anytime and anywhere. This cannot be guaranteed for sequences extracted by electrophoresis and subsequent base calling as base probability values do not exist for every base calling method. The backbone strategy can also be easily affected by repetitive short and long subsequences in the target DNA if additional assembly support information is not available. On the other hand, once the backbone of the assembly has been constructed, adding more reads to reduce base calling errors step by step is trivial.

Increasing the coverage of a contig first - by adding reads containing mostly sequences already known - ensures that the base qualities of the consensus raise rapidly: more reads that cover a consensus position make consensus errors introduced by bad signal quality and subsequent base calling errors increasingly improbable. Reads added afterwards have thus an increasing probability to align against a right consensus sequence. The disadvantage of this method appears when parts of a contig are only covered by low to medium quality reads. The increased coverage results in a growing number of discrepancies between read bases, leading to incorrect an consensus and sometimes stopping the assembler from adding reads to a contig where there is theoretically a possibility to continue.

Path traversal strategies

Figure 30: Example for an assembly graph (to be studied together with figure 31 on page that causes problems when using a simple greedy algorithms, assuming that read B is a chimeric sequence.

The assembly graphs build in the previous step have the unpleasant characteristic to be quite large even for small assemblies. In case of multiple - almost identical - repeats, the number of edges present in the graph explodes. Figure 30 shows a part of a much bigger graph used as example in this section.

Simple greedy algorithm

A simple greedy algorithm was first tried to find overlap candidates in the assembly graph, but on occasions - especially in highly repetitive parts of a genome or with chimeric reads²⁵ in low coverage sequencing - this algorithm fails. Figures 30 and 31 demonstrates how the simple greedy algorithm in conjunction with a chimeric read can provoke the termination of contig building while there exist possibilities to extend it further. This also corresponds to the results that have been reported previously by Myers (1994).

Figure 31: Example continued from figure 30 for a failure of the simple greedy algorithm (left side): read B is a chimeric read that has a strong overlap with read A, but would lead into a dead end of the assembly. A recursive look ahead strategy discovers contradictions between reads before they are assembled (right side): read B is automatically not used in the assembly.

n, m-step recursive look-ahead strategy

The current algorithm is an extension of the greedy algorithm. The pathfinder will search for the n best edges leading from nodes that are already inserted in the contig to nodes that have not been used yet. These n new nodes are inserted in n partial look-ahead paths as potential next alignment candidates. Each partial path is then descended recursively for a maximum of m recursions, repeating in each step the selection of the n next best edges. In the end the pathfinder designates the next read to add to an existing contig by taking the edge leading to the first node that is contained in the best partial path found so far, i.e., the partial path with the best summed score of its edges wins. It then presents the read which the edge led to - and its approximate position - to the contig object as potential candidate for inclusion into the existing consensus.

By performing an in-depth analysis - with a cutoff value of normally 4 or 5 recursions - of the weights to neighbouring reads contained in the assembly graph, the n, m recursive look-ahead strategy can substantially reduce the number of misalignments as chimeric reads get only a very small chance of getting aligned. At the same time, reads containing repetitive elements will not get aligned without 'approval' from reads already in the contig and reads to be aligned afterwards.

Contig

A contig is represented by a collection of reads that have been arranged in a certain order with given offsets to form an alignment that is optimal. The problem lies in the definition 'optimal' as different criteria like length, coverage, number of inconsistencies and others can be applied. The usual definition of an SCS (shortest common superstring) alignment given in literature leads in many cases to over-compressed alignments, especially when repeats are present. On the other hand, defining an alignment to be optimal when it has the least possible number of inconsistencies leads to alignments that are too long.

To elude these problems known in literature, an alignment has been defined to be optimal when the reads forming it have as few unexplained errors as possible but still form the shortest possible alignment.

For this purpose the contig object has been provided with functions that analyse the impact of every newly added read (at a given position) on the existing consensus. The assumption is now that - as the assembly presumably started with the best overlapping reads available - the bases in the consensus will be right at almost every position. Should the newly added read integrate nicely into the consensus, providing increased coverage for existing consensus bases and perhaps extending it a bit, then the contig object will accept this read as part of the consensus.

In some cases the assembly graph will contain chance overlaps between otherwise unrelated reads. Should such an overlap be good enough to be chosen by the pathfinder algorithm as next alignment candidate, the read will most probably differ in too many places from the actual consensus (thus differing in many aspects from reads that have been introduced to the consensus before). The contig will then reject the read from its consensus and tell the pathfinder object to search for alternative paths through the weighted overlap graph. The pathfinder object will eventually try to add the same read to the same contig but at a different position or - skipping it - try other reads.

Once the pathfinder has no possibilities left to add unused reads to the actual contig, it will again search for a new anchor point and use this as starting point for a new contig. This loop continues until all the reads have been put into contigs or - if some reads could not be assembled anywhere - form single-read contigs.²⁶

Contig approval methods

Myers et al. (1996) proposed using constraints in progressive multiple alignment. The idea has been extended toward the object acceptance method described in this section. As mentioned briefly above, each contig object has the possibility to reject a read being introduced into its consensus. This is one of the most crucial points in the development of the assembler: allowing presumably good building blocks, i.e. reads with high quality, to start an assembly is a decisive step in the ongoing assembly process, but the contig must actively decide upon all available data if the reads proposed to it are good enough to be assembled. This allows to use explicit knowledge available in reads that are known to be good and the implicit knowledge present in the assembly.

Figure 32: Assembly graph from figure 29 used as example in section 4.4.4.

The simplest behaviour of a contig could be to simply accept every new read that is being presented as part of the consensus without further checks. In this case the assembler would thus rely only on the weighted graph, the method with which the weighted edges were calculated and the algorithm which traverses this graph. Figure 33 shows this exemplarily for the reads from the example set up above. Although there are four columns having discrepancies, the assembly looks quite reasonable.

Figure 33: Example of simplest possible assembly which does not take advantage of additional knowledge. Reads are assembled as the algorithm walks through the path, the checkmarks showing the reads have been accepted as matching to the contig. Black squares mark discrepancy columns not having the same bases. Continued in figure 34.

Acceptance upon actual consensus constraints

Every read added to a contig must match the consensus build by previously inserted reads. As the overall working mechanism of the assembly algorithm will insert reads with good quality and strong overlaps into a contig first, there is a reasonable chance to believe that the actual consensus formed by these reads is quite correct up to a certain threshold.

If a newly inserted read shows too many discrepancies to the actual consensus sequence, the contig will invariably reject this read and the edge representing the corresponding overlap will be removed from the assembly graph. The main reasons for overlaps of this type being present in the assembly graph include spurious matches that slipped through Smith-Waterman, repetitive sequence and chimeric reads.

Repeat marker tags

However, using additional information that is available at the time of assembly proves useful. For example, known standard repetitive elements - e.g. the so called ALU repeat type in human genome - can easily be tagged in the data preprocessing step of the assembly. It is therefore possible to apply much stricter control mechanisms in those stretches of a sequence known to be repetitive and therefore dangerous to the assembly process. In many cases, the copies present across different regions of a genome are up to 98% to 99% similar, hence the necessity to be able to decide upon a few bases that might really differ.

In case of repetitive sequences, each discrepancy between a newly inserted read and the actual consensus is treated as single-base error region, i.e. the explanation of the possible base-call error to be analysed has to be searched in the immediate vicinity of the base. The question the simple signal analysis (see the following section) has to answer is if whether or not it is possible - that is, if there is enough evidence in the trace data - to substitute the offending base of the new read against the base calculated in the consensus. If signal analysis reveals that it is possible to substitute bases, the error is treated as 'explainable' error and it is treated as 'unexplainable' if not.

If the percentage of 'unexplainable' errors in the repetitive region surpasses a certain threshold (default value is 1%), then the newly inserted read will be rejected from the consensus and its node put back into the assembly graph as shown in figure 34.

Figure 34: Using additional information on standard repetitive stretches, the contig object checks the repeat regions more thoroughly and rejects reads that have too many errors that cannot be explained by signal analysis. Example continued in figure 35 on page .

Simple signal analysis

The best method to adjudicate on conflicting bases of different reads is to perform signal analysis, going back to the original trace data produced by the sequencing machines. This labour intensive task is normally executed by highly trained personnel although in a significant number of cases it is fairly easy to decide on conflicting readings by analysing the trace data.

Two different computational methods have been established in the past years to adjudicate om conflicting bases in reads. The probably most common method is the usage of quality values first introduced by Staden (1989) and further developed by Bonfield et al. (1995a). The concept was then refined to probability values by Ewing and Green (1998). Base probability values are experimentally gained, position-specific probabilities of error for each base-call in a read as a function of certain parameters computed from trace data. Probability values are of high value for finding bases with weak quality, but these values are mostly only available for the called bases, not for uncalled ones. For an assembler, it is a big drawback not to have the capability to search for alternative base-calls that might have been possible at the same position in the trace.

Another suggestion on incorporating electrophoresis data into the assembly process promoted the idea of capturing intensity and characteristic trace shape information and provide these as additional data to the assembly algorithm (Allex et al. (1997,1996)). Although methods for storing alternative base calls and other data have been suggested (Walther et al. (2001)), the approach from Ewing and Green (1998) produces results that are simple to handle and apparently 'good enough' so that it has imposed itself as standard over the years.

Complex shape approaches were discarded early in development of the algorithms for the assembler as essentially all the contig - and with it the consensus computing algorithm of a contig - needs to know is if the signal analysis reveals enough evidence for resolving a conflict between reads by changing the bases incriminated. This question is a simple working hypothesis which is a subset of the hypotheses generated by the automatic editor devised by Pfisterer and Wetter (1999).

It is possible to call the automatic editor in analysis mode to have this specific questions analysed. The conditio sine qua non for the assembly algorithm is that the signal analysis does not try to find support for a change of the possibly faulty base with ``brute force''. This would lead into the doctrine to use high quality sequence to adjust presumably low quality sequence, which is a complete contradiction of the working principle of using high quality data to explain errors in low quality sequences and correct them only if the low quality data supports the new theory.

In fact, the analysis is executed with the uttermost cautiousness and the signal analyser will support a base change only if hard evidence for this hypothesis can be found in the trace signals. Otherwise the assembler treats signal analysis as a black box decision formed by an expert system, only called during the assembly algorithm when conflicts arise. But this expert system provides nevertheless additional and more reliable information than the information contained in quality values extracted from the signal of one read only (compare to Durbin and Dear (1998)): there is a reasonable suspicion deduced from other aligned reads on the place and the type of error where the base caller could have made a mistake by analysing only a single read.

Figure 34 shows this information - along with a new assembly that took place - using the knowledge that repetitive elements must be checked much more strictly. In this new assembly, read 5 and read 4 were rejected from the contig as the pathfinder tried to enter them, because they induced errors into the already existing contig formed by the reads 2-1-3 (when adding read 5) and 2-1-3-6 (when adding read 4).

Figure 35: Example continued from figure 34 on page . Using strict signal checking in the ALU repeat region, unexplained errors in a first iteration of the assembler lead to the formation of two contigs in the second iteration. In this second iteration, no unexplained errors remain in the ALU region which is known as dangerous. Example continued in figure 39 on page .

The contig object failed to find a valid explanation to this problem when calling the signal analysis function - provided by the automatic editor - that tried to resolve discrepancies by investigating probable alternatives at the fault site. Figure 35 shows the result of the assembly that began in figure 34. There is not enough evidence found in the conflicting reads to allow a base change to resolve the discrepancies arising. There is also the additional knowledge that these non-resolvable errors occur in an area tagged as 'ALU-repeat', which leads to a highly sensitive assessment of the errors. Consequently, the reads 4 and 5 - containing repetitive sequence which the first contig object could not make match to its consensus - form a second contig as shown in the example.

Template size constraints

Large scale sequencing projects nowadays mostly use dual ended sequencing techniques as they provide valuable supplementary layout information for little cost overhead. With this technique both ends of a subclone (template) are sequenced so that normally two reads are generated for each template. Using short subclones of approximately 2 kilobases there is even a good probability that the reads will overlap in their ends.

The first constraint that can be deduced from this is the fact that - whenever the two reads belonging to a template can be inserted into the same contig - both reads have to be on opposite strands. As the approximate template size is also known, the second - equally important constraint - specifies a size range for both reads belonging to a template to be placed in the contig.

Large projects²⁷ are often sequenced using subclone libraries of different sizes. This can be done purposely to help building assembly scaffolds solely from overlap information and size constraints (Gene Myers' keynote on the German Conference on Bioinformatics (GCB) 99: ''A Whole Genome Assembler for Drosophila''). It can also be a direct implication of the re-sequencing of certain parts of a project.²⁸ The insert size of a template is therefore a template specific information that must be read from experiment files as additional assembly information and cannot be given as general parameter.

If the read is the first of a template to be inserted, the contig will accept it without checking template constraints. In case the newly added read is the second, the contig will check the constraints discussed above and reject the read if either one is not fulfilled.

Consensus and consensus quality computation

Calculating the consensus and its quality is not trivial and many groups have proposed different strategies, ranging from the simplest sum-of-scores to algorithms using simulated annealing (Keith et al. (2002)), none of which is really optimal when base error probability values are available. The method developed for this thesis has a basic idea which is quite simple: go through each column of an alignment, calculate a group quality for each base and take the base with the highest group quality. The quality values of bases encode - if present - error probabilities, which in turn are used to give an assessment of the quality of the consensus base they are part of. Using the definition of alignments in chapter 2 where an alignment L is

$$\bf L \left(\vphantom{ \begin{array}{ccc} s_{11} & \ldots & s_{1n}\\ \vdots & \ddots & \vdots\\ s_{k1} & \ldots & s_{kn}\\ \end{array}}\right. \begin{array}{ccc} s_{11} & \ldots & s_{1n}\\ \vdots & \ddots & \vdots\\ s_{k1} & \ldots & s_{kn}\\ \end{array} \left.\vphantom{ \begin{array}{ccc} s_{11} & \ldots & s_{1n}\\ \vdots & \ddots & \vdots\\ s_{k1} & \ldots & s_{kn}\\ \end{array}}\right)$$ =

with each element $s_{ij} \in \ensuremath{\mathcal{A}^{G}}$. A single column at position i within that alignment is defined as

$$\bf C_i \left(\vphantom{ \begin{array}{c} s_{1i} \\ \vdots \\ s_{ki} \\ \end{array}}\right. \begin{array}{c} s_{1i} \\ \vdots \\ s_{ki} \\ \end{array} \left.\vphantom{ \begin{array}{c} s_{1i} \\ \vdots \\ s_{ki} \\ \end{array}}\right)$$ =

which can also be seen as a simple vector. For the sake of simplicity, the vector only contains bases from $\ensuremath{\mathcal{A}^{g}}$ instead of $\ensuremath{\mathcal{A}^{G}}$ as endgaps ($\nabla$) do not really count as valid character.

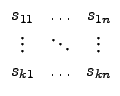Two more vectors can be defined by recording the error probability for each base and the direction of each sequence in the alignment:

$$\bf P_i \left(\vphantom{ \begin{array}{c} p_{1i} \\ \vdots \\ p_{ki} \\ \end{array}}\right. \begin{array}{c} p_{1i} \\ \vdots \\ p_{ki} \\ \end{array} \left.\vphantom{ \begin{array}{c} p_{1i} \\ \vdots \\ p_{ki} \\ \end{array}}\right)$$ =

and

$$\bf D \left(\vphantom{ \begin{array}{c} s_{1} \\ \vdots \\ s_{k} \\ \end{array}}\right. \begin{array}{c} s_{1} \\ \vdots \\ s_{k} \\ \end{array} \left.\vphantom{ \begin{array}{c} s_{1} \\ \vdots \\ s_{k} \\ \end{array}}\right)$$ =

Note that the $\bf D$ vector does not need to be made for each column separately as - understandably - sequences in an alignment have exactly one direction which does not change for each base.

Should discrepancies in the called bases occur in this column, the probability for an error will be computed for each base character group separately. Two main points must be considered when setting up a formula to compute this probability:

• there must be a limit in the number of error probabilities used to prevent overrepresented bases - but with a high error probability - to take advantage over a low number of bases with low error probabilities. This is a problem especially encountered in non-normalised EST projects.
• probabilities coming from different sequencing directions should deserve a higher weigh than those coming from the same direction. This is a tribute to the sequencing methods currently used as there are sometimes sequence specific problems occurring.²⁹ Fortunately, when the other strand is sequenced, most - if not all - problems related to this will vanish.

As a first step, the probability values can be grouped together by base and direction of the sequence in the alignment:

$$\mbox{\Huge {$\forall$}}$$

c $$\in$$ $$\mathcal {A}$$^b

P_i(c)⁺ = $$\left(\vphantom{ \begin{array}{c} p_{1i} \\ \vdots \\ p_{ki} \\ \end{array}}\right.$$$$\begin{array}{c} p_{1i} \\ \vdots \\ p_{ki} \\ \end{array}$$$$\left.\vphantom{ \begin{array}{c} p_{1i} \\ \vdots \\ p_{ki} \\ \end{array}}\right)$$        with        s_xi = c    and    D(s_x) = +

and

$$\mbox{\Huge {$\forall$}}$$

c $$\in$$ $$\mathcal {A}$$^b

P_i(c)^- = $$\left(\vphantom{ \begin{array}{c} p_{1i} \\ \vdots \\ p_{ki} \\ \end{array}}\right.$$$$\begin{array}{c} p_{1i} \\ \vdots \\ p_{ki} \\ \end{array}$$$$\left.\vphantom{ \begin{array}{c} p_{1i} \\ \vdots \\ p_{ki} \\ \end{array}}\right)$$        with        s_xi = c    and    D(s_x) = -

E.g., all bases with an A from sequences in forward direction are taken together in the P_i(A)⁺ group probability, bases with an A from sequences in reverse complement direction are taken in the P_i(A)^- group probability.

Each of the P_i(c) vectors is now sorted by value from low to high. The results are sorted vectors PS of error probabilities, for each base and each direction one.

PS_i(c) = sort(P_i(c))

Figure 36: Simple example for calculating the group quality of base column. For the sake of simplicity, the vectors for the bases (C), their directions (D) and error probabilities (PS_G(A)) were already sorted by the probability values. The n factor has been set to 10 in this example, meaning that none of the vectors had to be pruned.

For the next step, the vectors are pruned to contain a maximum of n lowest probability entries. The motivation for this step is loosely modeled after the entropy calculation theorem of the information theory. Grossly oversimplified, this theorem stipulates that the more information snippets sustaining one single fact are present, the less a single snippet of information itself is worth. Once the probability vector was sorted by value with the lowest values first, taking only the first n lowest values discards only those error probabilities that would not add much to the information itself.

In the next step, the inverse of the probability values are summed up, starting with the highest inverse and modifying the values with a decreasing scalar:

I_G(c)^+/- = $${\frac{{n}}{{n}}}$$$${\frac{{1}}{{PS_1(c)^{+/-}}}}$$ + $${\frac{{n-1}}{{n}}}$$$${\frac{{1}}{{PS_2(c)^{+/-}}}}$$ + ... + $${\frac{{1}}{{n}}}$$$${\frac{{1}}{{PS_n(c)^{+/-}}}}$$

The formula above ensures that the lowest error probability adds most of the information, with the following probabilities adding less and less until trailing off to zero. The probability for each directed base group is computed with the inverse of I(c):

P_G(c)^+/- = $${\frac{{1}}{{I_G(c)^{+/-}}}}$$

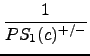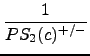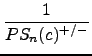
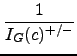
As last step, the total group error probability is computed by multiplying both directed group probabilities:

P_G(c) = P_G(c)⁺*P_G(c)^-

with the special cases that P_G(c)^+/- = 1 for each of the non-existing directed quality groups and P_G(c) = 0 if both do not exist. See figure 36 for an example.

Once such a group quality has been computed for every base character of a column, the character with the highest group quality wins and is taken as consensus base for this column. When using IUPAC consensus characters, base characters with a certain minimum group quality - e.g. an error probability of less than 0.001 which equals a quality value of 30 and more - are taken to form the IUPAC consensus base.